Основные определения
Существует довольно много равносильных определений деревьев, вот лишь некоторые из них.
- Дерево - это связный граф без циклов.
- Дерево - это связный граф, в котором при N вершинах всегда ровно N-1 ребро.
- Дерево - это граф, между любыми двумя вершинами которого существует ровно один путь.
Аналогичным образом определяется и ориентированное дерево - как орграф, в котором между любыми двумя вершинами существует не более одного пути.
| Армия | Солдаты и офицеры | Иерархия (командир - подчиненный) |
| Династия (родословная по мужской4 линии) | Монархи | Отношение "отец - сын" |
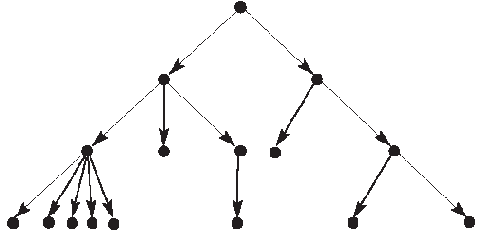
Рис. 11.12. Корневое дерево высоты 3
Мы будем изучать и использовать только один частный случай ориентированных деревьев - корневые деревья (см. рис. 11.12).
Корневое дерево - это ориентированное дерево, в котором можно выделить вершины трех видов: корень, листья (другое их название: терминальные вершины) и остальные вершины (нетерминальные); причем должны выполняться два обязательных условия:
- из листьев не выходит ни одна дуга; из других вершин может выходить сколько угодно дуг;
- в корень не заходит ни одна дуга; во все остальные вершины заходит ровно по одной дуге.
Традиционно в математике и в родственных ей науках (в том числе и в теоретическом программировании) деревья "растут" вниз головой: это делается просто для удобства наращивания листьев в случае необходимости. Таким образом, на рисунках корень дерева оказывается самой верхней вершиной, а листья - самыми нижними.
Предок вершины v - это вершина, из которой исходит дуга, заходящая в вершину v. Потомок вершины v - это вершина, в которую заходит дуга, исходящая из вершины v. В этих терминах можно дать другие определения понятиям корень и лист: у корня нет предков, у листа нет потомков.
Бинарное дерево - это корневое дерево, каждая вершина которого имеет не более двух потомков. В таком случае иногда говорят о левом потомке и правом потомке для текущей вершины.
Высота корневого дерева - это максимальное количество дуг, отделяющих листья от корня. Если дерево не взвешенное, то его высота - это просто расстояние от корня до самого удаленного листа.
И в заключение мы приведем определение, связывающее произвольные графы с деревьями более плотно.
Каркас графа - это дерево, полученное после выбрасывания из графа некоторых ребер (см. рис. 11.13).
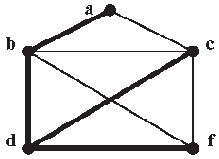
Рис. 11.13. Каркас графа
Примером каркаса является (корневое) дерево кратчайших путей от некоторой выделенной вершины (она будет корнем каркаса) до всех остальных вершин графа.
