Дерево двоичного поиска
Дерево двоичного поиска для множества чисел S - это размеченное бинарное дерево, каждой вершине которого сопоставлено число из множества S, причем все пометки удовлетворяют следующим условиям:
- существует ровно одна вершина, помеченная любым числом из множества S;
- все пометки левого поддерева строго меньше, чем пометка текущей вершины;
- все пометки правого поддерева строго больше, чем пометка текущей вершины.
Если выражаться простым языком, то структура дерева двоичного поиска подчиняется простому правилу: "если больше - направо, если меньше - налево".
Например, для набора чисел 7, 3, 5, 2, 8, 1, 6, 10, 9, 4, 11 получится такое дерево (см. рис. 11.14).
Для того чтобы правильно учесть повторения чисел, можно ввести дополнительное поле, которое будет хранить количество вхождений для каждого числа.
Более подробно процессы построения и анализа дерева бинарного поиска будут изложены в следующей лекции, посвященной алгоритмам, использующим деревья и графы.
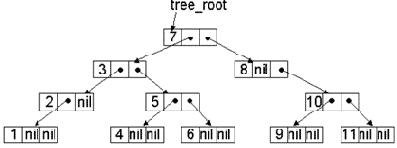
Рис. 11.14. Дерево двоичного поиска
